Question

A buoy floats on the surface of the water. The height in meters of the buoy 't' hours after midnight, relative to sea level, is given by the equation f(x) = 5cos(pi/6)t + 4. Estimate how many hours elapse between the first two times the buoy is exactly 6 m above sea level.

a.) 2.2 hours
b.) 5.8 hours
c.) 6.4 hours
d.) 7.6 hours

Answer 1

I think it's B. 5.8 hours. ;)

Answer 2

Option: d is the correct answer.

d.) 7.6 hours

Explanation:

We are given a function f(t) that represents the height in meters of the buoy 't' hours after midnight, relative to sea level.

`f(t)=5\cos ((\pi)/(6))t+4`

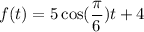
Now, we are asked to find the hours elapse between the first two times the buoy is exactly 6 m above sea level.

i.e. we have to find the difference between two consecutive times such that:

f(t)=6.

Now, we could see this with the help of the graph of the function to find the first two point at which the function receives the value 6.

Clearly from the graph we could see that the first time when f(t)=6 is:

t=2.214

and the second time when f(t)=6 is:

t=9.786

Hence, the elapse in the time is:

9.786-2.214

= 7.572 hours.

which is approximately equal to:

7.6 hours.

Hence, option: d is the answer.