Question

Follow the steps in hypothesis testingA manufacturer contemplating the purchase of new tool making equipment has specified that, on average, the equipment should not require more than 10min of setup time per hour of operation. The purchasing agent visits a company where the equipment being considered is installed; from records there the agent notes that 25 randomly selected hours of operation included a total of 4hr and 30min of setup time, and the standard deviation of setup time per hour was 3.0 min. Based on this sample result, can the assumption that the equipment meets setup time specifications be rejected at the .05 percent level of significance?

Answer 1

We will accept the null hypothesis and conclude that the equipment meets setup time specifications

Hence, the assumption cannot be rejected

Step-by-step explanation:

Firstly, we set up the null and alternative hypotheses as follows:

`\begin{gathered} H_0\text{ : }\mu\text{ }\leq\text{ 10} \\ H_1\text{ : }\mu\text{ }>\text{ 10} \end{gathered}`

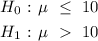
The null hypothesis states that the average set-up time should not be more than 10 min while the alternative states otherwise

Now, we proceed to calculate the test statistic value as follows:

We use the t-test :

`t\text{ = }\frac{x_(-bar)\text{ - }\mu}{(\sigma)/(√(n))}`

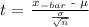
where:

x_bar represents total operation time divided by the total number if samples which is 4 hr 30 min = 4(60) + 30 = 270/25 minutes = 10.8

we have the mean value as 10 minutes

We have the standard deviation as 3 minutes

We have the number of samples as 3 minutes

Substituting the values, we have the t value as:

`\begin{gathered} t\text{ = }(10.8-10)/((3)/(√(25))) \\ \\ t\text{ = }(0.8)/((3)/(5))\text{ = }(0.8)/(0.6)\text{ = 1.333} \end{gathered}`

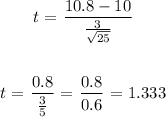
Now, we proceed to get the degree of freedom

That would be the number of samples 25 - 1 = 24

We can then get the t-value from the test statistic table

This gives us: 0.09801

From what we have here, the t-value is greater than the level of significance (0.05), we can conclude the following:

" We will accept the null hypothesis and conclude that the equipment meets setup time specifications"