Answer:
We will accept the null hypothesis and conclude that the equipment meets setup time specifications
Hence, the assumption cannot be rejected
Step-by-step explanation:
Firstly, we set up the null and alternative hypotheses as follows:
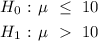
The null hypothesis states that the average set-up time should not be more than 10 min while the alternative states otherwise
Now, we proceed to calculate the test statistic value as follows:
We use the t-test :
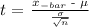
where:
x_bar represents total operation time divided by the total number if samples which is 4 hr 30 min = 4(60) + 30 = 270/25 minutes = 10.8
we have the mean value as 10 minutes
We have the standard deviation as 3 minutes
We have the number of samples as 3 minutes
Substituting the values, we have the t value as:
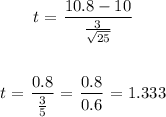
Now, we proceed to get the degree of freedom
That would be the number of samples 25 - 1 = 24
We can then get the t-value from the test statistic table
This gives us: 0.09801
From what we have here, the t-value is greater than the level of significance (0.05), we can conclude the following:
" We will accept the null hypothesis and conclude that the equipment meets setup time specifications"