Question

A mountain climber is at an altitude of 2.9 mi above the earth’s surface.

From the climber’s viewpoint, what is the distance to the horizon?

Answer 1

the answer is 151.6 hope this helps

Answer 2

Using Pythagoras theorem:

`\text{Hypotenuse side}^2 =\text{Adjacent side}^ + \text{Opposite side}^2`.

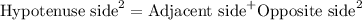We know that:

The radius of a circle meets a tangent at 90 degree

Labelled the triangle as A, B and C as shown below;

In rt angle triangle ABC:

Opposite side = AB = x units

Adjacent side = BC = 3959 mi

Hypotenuse side=AC = 3959 +2.9 = 3961.9 mi

Using Pythagoras theorem;

`AC^2 = BC^2+AB^2`

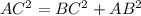
then;

`3961.9^2 = 3959^2+x^2`

`15696651.6 = 15673681+x^2`

⇒
`22970.6 = x^2`

⇒
`√(22970.6) = x`

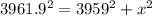
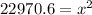
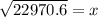
Simplify:

151.560549 = x

or

x = 151.6 mi

Therefore, the distance to the horizon From the climber’s viewpoint is, 151.6 mi