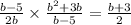Question

Find the simplified product b-5/2b x b^2+3b/b-5

Answer 1

Your answer should be A

Answer 2

The product
`(b-5)/(2b)*(b^2+3b)/(b-5)=(b+3)/(2)`

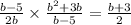
Explanation:

Given expression
`(b-5)/(2b)` and
`(b^2+3b)/(b-5)`

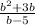
We have to find the product of
`(b-5)/(2b)*(b^2+3b)/(b-5)`

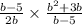
Consider the given expression
`(b-5)/(2b)*(b^2+3b)/(b-5)`

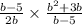
Multiply fractions, we have,

`(a)/(b)\cdot (c)/(d)=(a\:\cdot \:c)/(b\:\cdot \:d)`

`=(\left(b-5\right)\left(b^2+3b\right))/(2b\left(b-5\right))`

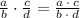
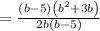
Cancel common factor ( b - 5 )

we have,
`=(b^2+3b)/(2b)`

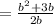
Apply exponent rule,

`\:a^(b+c)=a^ba^c`

`b^2=bb`

`=bb+3b=b(b+3)`

`=(b\left(b+3\right))/(2b)`

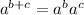
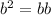
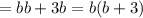
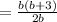
Cancel common factor b , we have,

`=(b+3)/(2)`

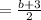
Thus, the product
`(b-5)/(2b)*(b^2+3b)/(b-5)=(b+3)/(2)`