Question

1. Solve for p

3(p + q) = p

2. Solve for b, then find the value of b when a = 3

4a = 2b - 7

3. Solve for r
d = rt

4. Find the width of a rectangle with a perimeter of 90 and a length of 15

A. 90
B. 15
C. 45
D. 30

Answer 1

`1. \quad p=(-3q)/(2)\\\\2. \quad b=(4a+7)/(2), b=(19)/(2)\\\\3. \quad r=(d)/(t)\\\\4. \quad \text{D. 30}`

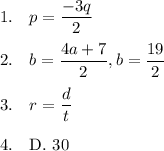
Explanation:

1. Subtract p:

3p +3q -p = 0

2p +3q = 0 . . . . collect terms

2p = -3q . . . . . . subtract 3q

p = -3q/2 . . . . . . divide by the coefficient of p

__

2. Add 7 and divide by the coefficient of b:

4a +7 = 2b

(4a +7)/2 = b

Substitute for a to find the value of b.

(4(3) +7)/2 = b = 19/2

__

3. Divide by the coefficient of r:

r = d/t

__

4. The sum of length and width is half the perimeter:

15 + w = 90/2 = 45

w = 30 . . . . . . . subtract the length; the width is 30 units