Question

Which best describes the graph of f(x) = log2(x + 3) + 2 as a transformation of the graph of g(x) = log2x?

Answer 1

3 units left

2 units up

Answer 2

3 unit left and 2 unit up.

Explanation:

Given :
`f(x)= \log_2(x + 3)+2` as a transformation of the graph of
`g(x) = \log_2x`

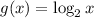
To find : Which best describes the graph transformation?

Solution :

The parent function
`g(x)=\log_2x`

with the vertex (1,0)

And the graph of
`f(x)=\log_2(x + 3)+2`

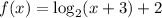
with the vertex (-2.75,0)

The graph of f(x) is the translation of g(x)

Transformation to the left,

f(x)→f(x+b) , the graph of f(x) is shifted towards left by b unit.

Same as the graph g(x) is shifted towards left by 3 unit and form graph of f(x).

`f(x)= \log_2(x + 3)`

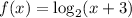
Transformation towards up,

f(x)→f(x)+a , the graph of f(x) is shifted upward by a unit.

Same as the graph g(x) is shifted upward by 2 unit and form graph of f(x).

`f(x)= \log_2(x + 3)+2`

Therefore, The description of the transformation is 3 unit left and 2 unit up.

Refer the attached graph below.