Question

Bernoulli differential equation... y'+xy=xy^2

Answer 1

`y'+xy=xy^2\implies y^(-2)y'+xy^(-1)=x`

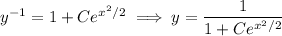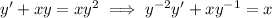
Let
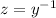
`z=y^(-1)`, so that
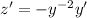
`z'=-y^(-2)y'`. Then the ODE becomes linear in
`z` with


`-z'+xz=x\implies z'-xz=-x`

Find an integrating factor:


`\mu(x)=\exp\left(\displaystyle\int-x\,\mathrm dx\right)=e^(-x^2/2)`

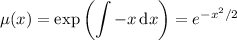
Multiply both sides of the ODE by
`\mu`:


`e^(-x^2/2)z'-xe^(-x^2/2)z=-xe^(-x^2/2)`

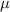
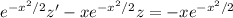
The left side can be consolidated as a derivative:


`\left(e^(-x^2/2)z\right)'=-xe^(-x^2/2)`

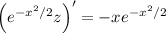
Integrate both sides with respect to
`x` to get


`e^(-x^2/2)z=e^(x^2/2)+C`

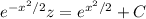
where the right side can be computed with a simple substitution. Then


`z=1+Ce^(x^2/2)`

Back-substitute to solve for
`y`.


`y^(-1)=1+Ce^(x^2/2)\implies y=\frac1{1+Ce^(x^2/2)}`