
notice above... we use the decimal format for the percentage, thus 20% is really just 20/100, 40% is 40/100 and so on.
so.. whatever "x" and "y" amounts are, we know they have to add up to 60 Liters, that is x+y = 60
and whatever the concentration amount of each is, it must add up to (60)(0.40), that is 0.20x+0.50y=(60)(0.40)
thus
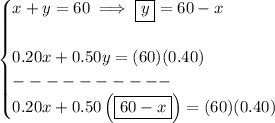
solve for "x", to see how much of the 20% solution will be needed
what about "y"? well, y = 60 - x