Question

What is the slant height of a square pyramid that has a surface area of 189 square feet and a side length of 7 feet? A. 14 ft B. 12 ft C. 10 ft D. 8 ft

Answer 1

C.) 10..........................

Answer 2

Answer: The correct option is (C). 10 feet.

Step-by-step explanation: We are given to find the slant height of a square pyramid that has a surface area of 189 square feet and a side length of 7 feet.

We know that the surface area of a square pyramid with base edge 'a' units and height 'h' units is given by

`A=a^2+2a\sqrt{(a^2)/(4)+h^2}.`

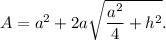
A square pyramid is shown in the attached figure.

In the given square pyramid, we have

length of the base edge, a = 7 feet,

Surface area, S.A. = 189 sq. ft.

If 'h' is the height of the pyramid, then we have

`A=a^2+2a\sqrt{(a^2)/(4)+h^2}\\\\\\\Rightarrow 189=7^2+2* 7\sqrt{(7^2)/(4)+h^2}\\\\\\\Rightarrow 189=49+14\sqrt{(49)/(4)+h^2}\\\\\\\Rightarrow 189-49=14\sqrt{(49)/(4)+h^2}\\\\\\\Rightarrow 140=14\sqrt{(49)/(4)+h^2}\\\\\\\Rightarrow 10=\sqrt{(49)/(4)+h^2}\\\\\\\Rightarrow 100=(49)/(4)+h^2\\\\\\\Rightarrow h^2=100-(49)/(4)\\\\\\\Rightarrow h^2=(351)/(4).`.

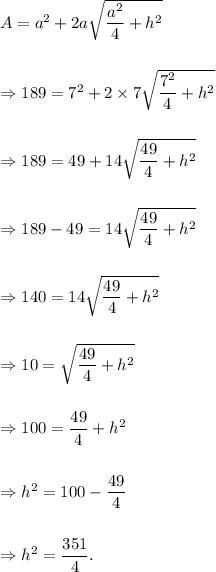So, if 'l' is the slant height of the pyramid, then

`l^2=h^2+\left((a)/(2)\right)^2\\\\\\\Rightarrow l^2=(351)/(4)+\left((7)/(2)\right)^2\\\\\\\Rightarrow l^2=(351)/(4)+(49)/(4)\\\\\\\Rightarrow l^2=100\\\\\Rightarrow l=10.`

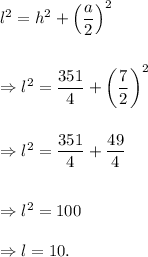
Thus, the slant height of the square pyramid is 10 feet.

Option (C) is correct.