Question

What does interior angle A of the polygon in the figure equal?

A. 230
B. 100
C. 110
D. 150

Answer 1

C.110 hopefully that's the right answer

Answer 2

The correct option is C.

Explanation:

The sum of interior angles of any polygon is defined as

`S=(n-2)* 180^(\circ)`

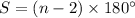
Where n is number of vertices of polygon.

From the given figure it is noticed that the number of vertices is 6. So, the sum of interior angles is

`S=(6-2)* 180^(\circ)=720^(\circ)`

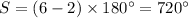
One exterior angle of 130 degree is given in the figure. So, the interior angle on that vertex is

`360-130=230`

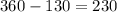
Now, add all the interior angles.

`S=50+100+120+A+110+230`

`S=A+610`

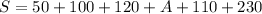
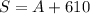
Since the sum of interior angles is 720, therefore

`720=A+610`

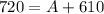
Subtract 610 from both sides.

`720-610=A+610-610`

`A=110`

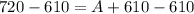
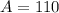
Therefore option C is correct.