Question

random variables, probability distributions and expected value Your brother has a bag of marbles containing 1 red marble, 2 blue marbles, and 47 green marbles. He claims he'll give you $10 if you pull the red marble but just $5 if you pull a blue marble. However, if you pull a green marble, you will owe him $3. What is the expected value each time you pull a marble? Round to the nearest cent. Do not round until your final answer.

Answer 1

To determine the expected value each time you pull a marble you have to construct a table of probability distributions.

Given the event "pull one marble of a determined colour"

For each marble colour there is a corresponding probability of appearence. To calculate said probability you have to divide the number of marbles of that colour by the total number of marbles in the bag.

The bag contains:

1 red marble

2 blue marbles

47 green marbles

The total number of marbles is then: 1+2+47=50

And the corresponding probabilities:

`\begin{gathered} P(red)=\frac{nº\text{red.marbles}}{\text{total.nºmarbles}}=(1)/(50) \\ P(blue)=\frac{nº\text{blue}\mathrm{}\text{marbles}}{total.nºmarbles}=(2)/(50) \\ P(gren)=\frac{nº\text{gren}\mathrm{}\text{marbles}}{\text{total}\mathrm{}nº\text{marbles}}=(47)/(50) \end{gathered}`

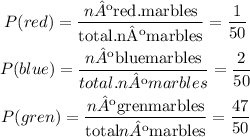
Now for each red marble you pull you'll gain $10, for each blue marble you'll gain $5 and for each green marble you'll owe $3.

Let X represent the "amount of money earned at the end of the game"

Note: the first value is red because you loose 3 dollars for each green marble, "-$3"

With the probability distribution determined you can calculate the expected value (i.e. mean value) using the following formula:

`X\lbrack bar\rbrack=\Sigma(X_i\cdot P(X_i))`

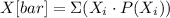
You have to multiply each value of X by its corresponding probability and add them:

`\begin{gathered} X\lbrack bar\rbrack=(-3\cdot(47)/(50))+(5\cdot(2)/(50))+(10\cdot(1)/(50)) \\ X\lbrack bar\rbrack=-(141)/(50)+(1)/(5)+(1)/(5) \\ X\lbrack bar\rbrack=-(121)/(50) \\ X\lbrack bar\rbrack=-2.42 \end{gathered}`

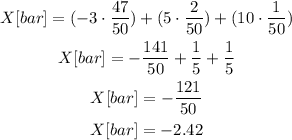
At the end of the game the expected earnings are -$2.42, this means that you'll owe your brother money.