Hello!
The figure is made up of a cone and a hemisphere. To the nearest whole number, what is the approximate volume of this figure? Use 3.14 to approximate π . Enter your answer in the box. cm³
A 12 cm cone with a dome on top of it that has an 8 cm diameter
Data: (Cone)
h (height) = 12 cm
r (radius) = 4 cm (The diameter is 8 being twice the radius)
Adopting:

V (volume) = ?
Solving:(Cone volume)
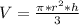

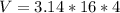
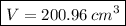
Note: Now, let's find the volume of a hemisphere.
Data: (hemisphere volume)
V (volume) = ?
r (radius) = 4 cm
Adopting:

If: We know that the volume of a sphere is
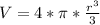 , but we have a hemisphere, so the formula will be half the volume of the hemisphere
, but we have a hemisphere, so the formula will be half the volume of the hemisphere
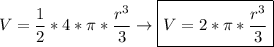
Formula: (Volume of the hemisphere)
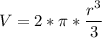
Solving:
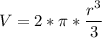
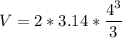
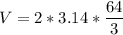
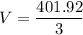

Now, to find the total volume of the figure, add the values: (cone volume + hemisphere volume)
Volume of the figure = cone volume + hemisphere volume
Volume of the figure = 200.96 cm³ + 133.97 cm³

________________________
I Hope this helps, greetings ... Dexteright02! =)