Question

Standing at a trailhead, you look up at a 54 degree angle and see your friend's cell phone reflecting the sun. You know that she is at the top of the 1200-foot cliff and you call her to say you'll meet her at the bottom of the cliff. How many feet will you have to walk to meet?

Answer 1

so check the picture below

recall your SOH CAH TOA
`\bf sin(\theta)=\cfrac{opposite}{hypotenuse} \qquad \qquad % cosine cos(\theta)=\cfrac{adjacent}{hypotenuse} \\ \quad \\\\ % tangent tan(\theta)=\cfrac{opposite}{adjacent}`

which identity uses only
angle
opposite
adjacent?

well, is Ms Tangent.. thus
`\bf tan(\theta)=\cfrac{opposite}{adjacent}\implies tan(54^o)=\cfrac{1200}{x}`

solve for "x", make sure your calculator is in Degree mode, since the angle is in degrees

Answer 2

The answer is 870 feet.

Explanation:

Let's make a diagram (look at the end of the explanation).

We can solve this problem by using trigonometry.

Recall the trigonometric ratios:

`sin(\alpha)=(opposite)/(hypotenuse)`

`cos(\alpha)=(adjacent)/(hypotenuse)`

`tan(\alpha)=(opposite)/(adjacent)`

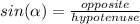
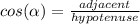
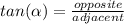
As we know the size of the opposite cathetus to
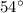`54^\circ` and we must work out the size of the adjacent cathetus (let's call it x), we can pick the tangent ratio (remember to use the degree -deg- mode of the calculator):

`tan(54^\circ)=(1200)/(x)`

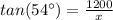
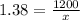`1.38=(1200)/(x)` (to 3 significant figures)

`1.38 x = 1200`

`x = 1200 : 1.38`

`x = 870`

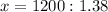
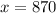
Therefore, you will have to walk 870 feet (to 3 sf) to meet your friend.