so hmm check the picture below
the diameter has those endpoints, recall the radius is half the diameter
the diameter length is
![\bf \textit{distance between 2 points}\\ \quad \\ \begin{array}{lllll} &x_1&y_1&x_2&y_2\\ % (a,b) &({{ 0}}\quad ,&{{ 4}})\quad % (c,d) &({{ 6}}\quad ,&{{ -4}}) \end{array}\qquad % distance value d = \sqrt{({{ x_2}}-{{ x_1}})^2 + ({{ y_2}}-{{ y_1}})^2}]()
the radius is half that
and the center will be half-way on that segment, namely, the MidPoint
so the center will be at
![\bf \textit{middle point of 2 points }\\ \quad \\ \begin{array}{lllll} &x_1&y_1&x_2&y_2\\ % (a,b) &({{ 0}}\quad ,&{{ 4}})\quad % (c,d) &({{ 6}}\quad ,&{{ -4}}) \end{array}\qquad % coordinates of midpoint \left(\cfrac{{{ x_2}} + {{ x_1}}}{2}\quad ,\quad \cfrac{{{ y_2}} + {{ y_1}}}{2} \right)\\\\ -----------------------------\\\\ h=\cfrac{{{ x_2}} + {{ x_1}}}{2}\qquad \qquad k=\cfrac{{{ y_2}} + {{ y_1}}}{2}]()
so plug those three
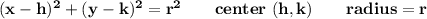
at