Either order is correct.
Small example: let's take

. Then
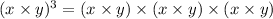
By the commutative property, we can write
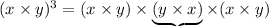
By the associative property, we can regroup consecutive terms.
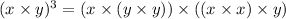
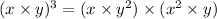
By the associative property again, we can regroup terms and write
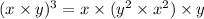
Commutativity:
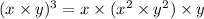
Associativity:
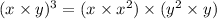
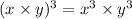
You can show by induction that this holds in general for

so that
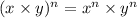
.