Question

Complete the square of x squared -2/5 x

Answer 1

`\bf \begin{array}{cccccllllll} {{ a}}^2& + &2{{ a}}{{ b}}&+&{{ b}}^2\\ \downarrow && &&\downarrow \\ {{ a}}&& &&{{ b}}\\ &\to &({{ a}} + {{ b}})^2&\leftarrow \end{array}\qquad % perfect square trinomial, negative middle term \begin{array}{cccccllllll} {{ a}}^2& - &2{{ a}}{{ b}}&+&{{ b}}^2\\ \downarrow && &&\downarrow \\ {{ a}}&& &&{{ b}}\\ &\to &({{ a}} - {{ b}})^2&\leftarrow \end{array}`

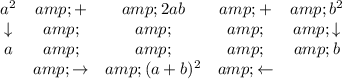
as you can see above... notice the middle term, in a perfect square trinomial, the middle term is, 2 times the guy on the left, without the exponent, and times the guy on the right

so.. .what we have here ... let's see yours is
`\bf x^2-\cfrac{2}{5}x\implies x^2-\cfrac{2}{5}x+\boxed{?}^2`

so.. we have a missing guy there, the guy on the right hmm what the dickens would that be anyway?

well... let us use the middle guy
`\bf 2\cdot x\cdot \boxed{?}=\cfrac{2}{5}x\implies \boxed{?}=\cfrac{2x}{10x}\implies \boxed{?}=\cfrac{1}{5}`

aha ... there's our guy on the right.... so now we know is 1/5

now... let us call or very good friend Mr Zero, 0

if we "add" whatever, we also have to "subtract" whatever, since all we're really doing is, borrowing from 0

thus
`\bf x^2-\cfrac{2}{5}x\implies x^2-\cfrac{2}{5}x\quad +\left( \cfrac{1}{5} \right)^2\quad -\left( \cfrac{1}{5} \right)^2 \\\\\\ \left[ x^2-\cfrac{2}{5}x +\left( \cfrac{1}{5} \right)^2 \right]-\left( \cfrac{1}{5} \right)^2\implies \left( x-\cfrac{1}{5} \right)^2 - \cfrac{1^2}{5^2} \\\\\\ \left( x-\cfrac{1}{5} \right)^2 -\cfrac{1}{25}`