Question

The area of a rectangular garden is given by the trinomial x^2+6x-27. what are the possible dimensions of the rectangle? use factoring

Answer 1

A = x^2 + 6x - 27 A = x^2 + 9x - 3x - 27 A = x(x+9)-3(x+9) A = (x+9)(x-3) A = lw l = (x+9) w =(x-3)

Answer 2

Explanation:

Given that a garden is in rectangular form

Area of the garden =
`x^2+6x-27`

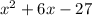
We know that area of a rectangle = length x width

Hence length x width =
`x^2+6x-27`

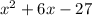
There can be infinite number of answers for this equation.

Let us assume that both length and width are rational.

Then the factors would be answers.

Factorise

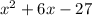`x^2+6x-27` as

`(x+9)(x-3)`

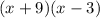
Since normally length would be longer, we can say

length = x+9 and width = x-3, for x >3.