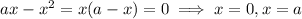
which means the parabola

intersects the x-axis at

and

. Assume
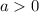
.
Then the volume of the solid generated by revolving the region about the x-axis is

Revolving about the y-axis, the volume would be

The volumes are the same independent of which axis is taken as the axis of revolution, so

We're assuming
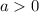
, so we can safely divide both sides by
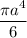
to get
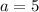
.