Question

1. The table below shows how the expected values of a computer and a printer vary with time. Time (years after purchase) Value of Computer Value of Printer 0 $960 $300 1 $720 $240 2 $540 $180 3 $405 $120 Based on the data in the table, which of the two devices decays in expected value by a constant percentage rate per year? How do you know? Think back to the wording we used in the warm up 2. Create an equation that represents the table from Question #1 (FLE 2)

Answer 1

The exponential decay formula is:

`y=a(1-r)^x^{}`

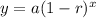
where y and x are the variables, a is the initial value, and r is the decay rate (as a decimal)

In the case of the values of a computer, the initial value is 960, that is, a = 960. y represents the value of the computer and x represents time. Substituting with x = 1, y = 720, and a = 960, we wet:

`\begin{gathered} 720=960\cdot(1-r)^1 \\ (720)/(960)=1-r \\ 0.75=1-r \\ r=1-0.75 \\ r=0.25 \end{gathered}`

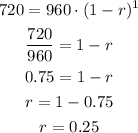
Now we can check if this model predicts correctly the other values of the table.

`\begin{gathered} y=960(1-0.25)^2=540 \\ y=960(1-0.25)^3=405 \end{gathered}`

These results show that the value of the computer decay by a constant percentage rate per year.

The equation is:

`y=960(1-0.25)^x=960(0.75)^x`