For asymptotes, we need to consider when a function becomes undefined.
Such examples include x = 0 as the denominator.
Vertical asymptotes are merely stated when an x-ordinate allows the function to become undefined. They are the easiest of the two to solve. Let's consider the first example:

In this case, we know that x is the denominator. So when the x-ordinate hits 0, there are no y-values to associate with the function. Hence, we know there is a vertical asymptote at x = 0.
Horizontal asymptotes are defined when a certain value of y makes the function undefined. They are usually harder to find and can be time-consuming. The easiest way to identify horizontal asymptotes is by taking limits or dividing a function.
Notice how our first section is 1/x. For harder polynomic functions, we would do something called long division of polynomials. But for this instance, let's divide the top and bottom of the fraction by x and take the limit as x approaches positive and negative infinite.
After division, we would get something like this:
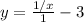
Now, as x approaches positive infinity, our fraction would get closer and closer to zero, so at x = infinity, our y value would be -3
At x = negative infinity, our y value would remain as -3.
So at x = infinity, we would yield y = -3, which is our horizontal asymptote.
So, VA: x = 0
HA: y = -3