For this case we know that the random variable x is given by:
X Unif(0,1)
The cumulative distribution function would be given by:
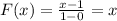
The correct graph would be:
First one
what is the probability of generating a number between .37 and .05?
For this case we can do the following:
0.37 -0.05 = 0.32
what is the probability of generating a number greater than .85?
For this case we can do the following:
P(X >0.85) = 1-P(X<0.85)= 1-0.85 = 0.15