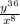Question

Simplify(x²y³(x⁰y⁻⁴)³)⁻⁴

Answer 1

Simplifying.

(x²y³(x⁰y⁻⁴)³)⁻⁴ =
`(y^3^6)/(x^8)`

Hope this helps!

Answer 2

y³⁶/x⁸

Step-by-step explanation

To simplify this expression we have to do it from the inner part of the expression to the outer part. First, we have x⁰, which is equal to 1,

`(x^2y^3(x^0y^(-4))^3)^(-4)=(x^2y^3(y^(-4))^3)^(-4)`

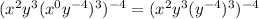
Then we have the interior parenthesis. To simplify this we have to apply the exponent of exponent rule,

`(a^b)^c=a^(b\cdot c)`

So we have,

`(x^2y^3(y^(-4))^3)^(-4)=(x^2y^3y^(-4\cdot3))^(-4)=(x^2y^3y^(-12))^(-4)`

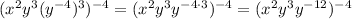
Next, apply the product rule of exponents with the same base,

`a^b\cdot a^c=a^(b+c)`

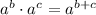
In this case,

`(x^2(y^3y^(-12)))^(-4)=(x^2y^(3-12))^(-4)=(x^2y^(-9))^(-4)`

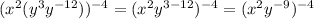
The exponents can be distributed into the multiplication, so we have,

`(x^2y^(-9))^(-4)=(x^2)^(-4)(y^(-9))^(-4)`

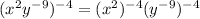
Apply the exponent of exponent rule again,

`(x^2)^(-4)(y^(-9))^(-4)=x^(2(-4))y^((-9)(-4))=x^(-8)y^(36)`

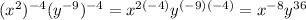
Finally, negative exponents flip the base,

`a^(-b)=(1)/(a^b)`

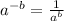
Hence, the simplified expression is,

`(y^(36))/(x^8)`