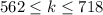Question

Tom owns two coin-laundry stores. The first store has between 89 and 122 loadsof laundry done on Thursday and between 119 and 153 loads of laundry onFriday. The second store has between 156 and 209 loads of laundry done onThursday and between 198 and 234 loads on Friday.If k represents the loads of laundry done, what inequality would represent thepossible range of the total number of laundry loads done at both stores on Thursdayand Friday?A/loads of laundry

Answer 1

Let T(1) and T(2) denote the load on the first and second store, respectively, on Thursday. While F(1) and F(2) denote the load on the first and second store, respectively, on Friday.

Given that load was between 89 and 122 on the first store on Thursday,

`89\leq T(1)\leq122\ldots\ldots\ldots(1)`

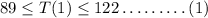
The load was between 119 and 153 on the first store on Friday,

`119\leq F(1)\leq153\ldots\ldots\ldots(2)`

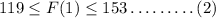
The load was between 156 and 209 on the second store on Thursday,

`156\leq T(2)\leq209\ldots\ldots\ldots(3)`

The load was between 198 and 234 on the second store on Friday,

`198\leq F(2)\leq234\ldots\ldots\ldots(4)`

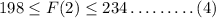
Now, we need to find the total number of laundry loads (k) on the two stores for Thursday and Friday combined,

`k=T(1)+F(1)+T(2)+F(2)`

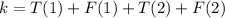
This can be obtained by adding the inequalities.

Consider that the inequalities having the same direction can be added directly. Since the inequalities (1), (2), (3), and (4) possess the same direction, they can also be added directly, and the resulting inequality becomes,

`\begin{gathered} (89+119+156+198)\leq T(1)+F(1)+T(2)+F(2)\leq(122+153+209+234) \\ 562\leq k\leq718 \end{gathered}`

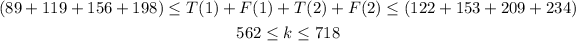
Thus, the required inequality for the total number of launYou're welcomdry loads done at both stores on Thursday and Friday is obtained as,

`562\leq k\leq718`