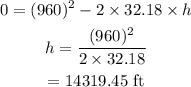Question

The huge Q36 pumpkin cannon is 80 feet long. It has a muzzle velocity of more than 960 feet per second. Wind resistance greatly reduces this nearly supersonic velocity.If fired straight up, what is the maximum height the pumpkin could reach? Ignore wind resistance. If fired straight up, approximately how long will the pumpkin be in the air? Again, ignore wind resistance.

Answer 1

Given:

The initial velocity of the pumpkin is

`v_o=960\text{ ft/s}`

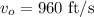
To find the maximum height of the pumpkin

and the time for which pumpkin will be air.

Step-by-step explanation:

When the pumpkin reaches maximum height its final velocity will be

`v_f=\text{ 0 ft/s}`

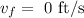
The equation used to calculate the maximum height will be

`v_f^2=v_o^2-2gh`

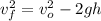
Here, the value of g is the acceleration due to gravity whose value is 32.18 ft/s^2.

On substituting the values, the maximum height will be

`\begin{gathered} 0=(960)^2-2*32.18* h \\ h=((960)^2)/(2*32.18) \\ =14319.45\text{ ft} \end{gathered}`