Question

A ball is dropped from the top of a building that is 1,000 feet high. Its height, in feet, as a function of the time, x, in seconds, after the ball was dropped, is given by the following equation, ƒ(x) = 1,000 - 16x 2. Which set of numbers is appropriate as the domain for this function?

Answer 1

Answer: The set of domain for the function is 0 ≤ x ≤ 7.906

Explanation:

Here, the given function that shows the distance of the ball from the surface after x seconds is,

`f(x) = 1000 - 16x^2`

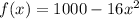
Since, the height can not be negative,

⇒ f(x) ≥ 0

`\implies 1000 - 16x^2\geq 0`

`\implies -16x^2 \geq - 1000`

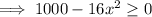
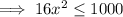`\implies 16x^2\leq 1000` ( x > y ⇒ -x < -y)

`\implies x^2 \leq (1000)/(16)`

`\implies x\leq \sqrt{{(250)/(4) }`

`\implies x\leq 7.906`

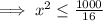
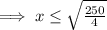
Also, x represents time,

⇒ 0 ≤ x,

Thus, the possible values of x are,

0 ≤ x ≤ 7.906

Since, all possible value of x = Domain of f(x)

⇒ Domain of f(x) is 0 ≤ x ≤ 7.906