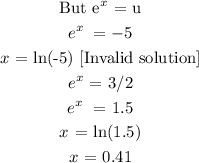Answer:
1) The equation rewritten as a quadratic equation in standard form using u-substitution is:
2u² + 7u - 15 = 0
2) The exact solution is:
x = 0.41
Explanations:
The qiven equation is:
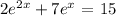
This can be rewritten as:
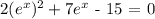
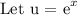
The equation rewritten as a quadratic equation in standard form becomes:
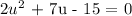
Factorize the quadratic equation above:
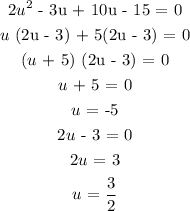
u = -5 or u = 3/2