Question

SOLVE THE SYSTEM OF EQUATIONS USING THE ELIMINATION METHOD {3/4x-2/7y=-5

{5/8x+1/4y=-3/4
Please show work so I can understand how to solve this problem.

Answer 1

`\bf \begin{cases} \cfrac{3}{4}x-\cfrac{2}{7}y=-5\\\\ \cfrac{5}{8}x+\cfrac{1}{4}y=-\cfrac{3}{4} \end{cases}`

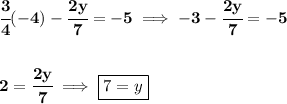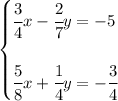
so... as you should know, the idea behind the elimination method, is to, eliminate one of the variables

and we'll do that, by multiplying either of the equations, by "something", so the value on top, resembles the one below, but of a different sign

let us eliminate "y" then.... and let us multiply the 1st equation by "something", we dunno what that is... but we want 2/7y to become 1/4y

that way, we'll end up with -1/4 y atop and +1/4y below, and those two added vertically, will simply give 0, thus "eliminating" "y"

let us start off by saying hmmm we don't want to hose the variable... so... let's say
`\bf \cfrac{2y}{7}=\cfrac{1}{4}\implies 2y=\cfrac{7}{4}\implies y=\cfrac{7}{8}`

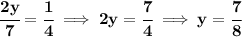
so... keeping the "y" variable, we'll just get a value to multiply by... so, it turns out, using that equation there, it ends up that, if we multiply 2/7 y times 7/8, we'll end up with 1/4 y, thus the idea behind the equating

now... we'll multiply the 1st equation then, all terms, by 7/8

thus we end up with
`\bf \begin{array}{llllll} \cfrac{21}{32}x&-&\cfrac{1}{4}y&=&-\cfrac{35}{8}\\\\ \cfrac{5}{8}x&+&\cfrac{1}{4}y&=&-\cfrac{3}{4}\\ --&--&--&--&--\\ \cfrac{41}{32}x&+&0&=&-\cfrac{41}{8}\impliedby \textit{their vertical sum} \end{array}\\\\ -----------------------------\\\\ \cfrac{41}{32}x=-\cfrac{41}{8}\implies \cfrac{41x}{32}=-\cfrac{41}{8}\implies x=-\cfrac{32\cdot 41}{41\cdot 8} \\\\\\ \boxed{x=-4}`

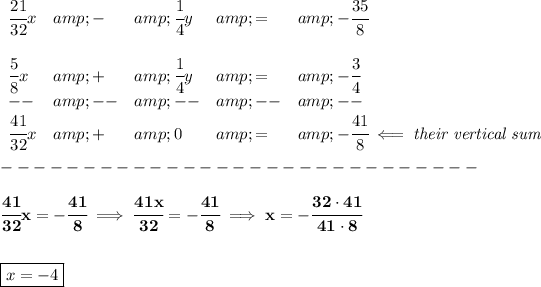
now that we know what "x" is, well, let us use that in either equation, and then solve for "y" then, hmmm let use the 1st equation then


`\bf \cfrac{3}{4}(-4)-\cfrac{2y}{7}=-5\implies -3-\cfrac{2y}{7}=-5 \\\\\\ 2=\cfrac{2y}{7}\implies \boxed{7=y}`