Question

Three charges, Q1, Q2, and Q3 are located in a straight line. The position of Q2 is 0.301 m to the right of Q1. Q3 is located 0.169 m to the right of Q2. The force on Q2 due to its interaction with Q3 is directed to the.....

1.Left if the two charges have opposite signs. t/f
2.Right if the two charges are negative. t/f
3.Left if the two charges are positive. t/f
4.Left if the two charges are negative. t/f
5. Right if the two charges have opposite signs. t/f
In the above problem, Q1= 1.90·10-6 C, Q2= -2.84·10-6 C, and Q3= 3.03·10-6 C.
1. Calculate the total force on Q2. Give with the plus sign for a force directed to the right.
2. Now the charges Q1= 1.90·10-6 C and Q2= -2.84·10-6 C are fixed at their positions, distance 0.301 m apart, and the charge Q3= 3.03·10-6 C is moved along the straight line. For what position of Q3 relative to Q1 is the net force on Q3 due to Q1 and Q2 zero? Use the plus sign for Q3 to the right of Q1.

Answer 1

Answer and Explanation: A charge exerts a force over another charge even if they are very far apart. This force is called Electrostatic Force.

If the two charges have the same sign, e.g. both aare positive, the force between them is opposite. If they have opposite sign, the force is towards each other. In other words, for electrostatic force, equal charges repel and different charges attract.

So,

1. If Q2 and Q3 have opposite signs, it is TRUE force in Q2 will go the left;

2. If the 2 are negative, they have the same sign, so it's FALSE force is to the right;

Sentences 3 and 4 are also TRUE due to the reasons described above;

5. If the charges have opposite signs, it means force is towards each other, or, to the right, so the sentence is TRUE;

1. Force is directly proportional to charges in Coulomb [C] and inversely proportional to distance squared in [m]:

`F=(k.q.Q)/(r^(2))`

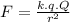
where k is a constant that equals 9 x 10⁹ N.m²/C²

Calculating force between 1 and 2:

`F_(12)=(9.10^(9)(1.9.10^(-6))(2.84.10^(-6)))/((0.301)^(2))`

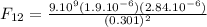
`F_(12)=536.02.10^(-3)` N

Force between 2 and 3:

`F_(23)=(9.10^(9)(2.84.10^(-6))(3.03.10^(-6)))/((0.169)^(2))`

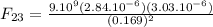
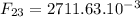`F_(23)=2711.63.10^(-3)` N

Total force is the net force. Since Q2 is negative and the others are positive, force of 2 related to 1 is to left and related to 3 is to the right. Therefore, total force is the difference between those two forces:

`F_(T)=2711.63.10^(-3)-536.02.10^(-3)`

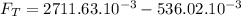
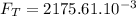`F_(T)=2175.61.10^(-3)` N

The total force on Q2 is 2175.61 x 10⁻³ N

2. For net force to be 0,
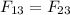`F_(13)=F_(23)`. Suppose distance from 1 to 3 is x, then from 2 to 3 is
`x-0.301`

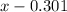
Calculating:

`(k(1.90.10^(-6))(3.03.10^(-6)))/(x^(2))=(k(2.84.10^(-6))(3.03.10^(-6)))/((x-0.301)^(2))`

`(5.757.10^(-12))/(x^(2)) =(8.6052.10^(-12))/(x^(2)-0.602x+0.090601)`

`(5.757.10^(-12))/(8.6052.10^(-12))=(x^(2))/(x^(2)-0.602x+0.090601)`

`x^(2)=0.67x^(2)-0.40x+0.061`

`0.33x^(2)+0.40x-0.061=0`

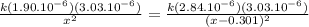
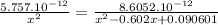
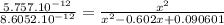
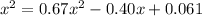
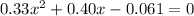
roots = 0.14 or -1.35

Solving quadratic equation gives 2 roots, but one of the roots is negative. As distance is a measure that cannot be negative, the solution is x = 0.14.

The distance of Q3 relative to Q1 is 0.14 m