Question

What is the sum of the finite arithmetic series 4+8+12+16...+76

Answer 1

a(n)=4+4(n-1)

a(n)=4+4n-4

a(n)=4n

76=4n

n=19

The sum of any arithmetic sequence (series are infinite) is:

(a+a(n))(n/2)

The average of the first and last terms times the number of terms, in this case we found that n=19 so:

19(4+76)/2=760

Answer 2

The nth term of the arithmetic sequence is given by:

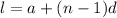`l= a+(n-1)d` .....[1]

and

the sum of the arithmetic sequence is:

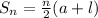`S_n = (n)/(2)(a+l)` .....[2]

where,

a is the first term

d is the common difference of two consecutive term

l is the last term in the series

As per the statement:

The finite arithmetic series 4+8+12+16...+76

here, a = 4 and

Common difference(d) = 4

Since,

8-4 = 4,

12-8 = 4,

16-12 = 4 and so on

last term of the finite series(l) = 76

Substitute these in [1] we have

`76 = 4+(n-1)4`

Using distributive property,
`a \cdot (b+c) =a\cdot b+ a\cdot c`

`76 = 4+4n -4`

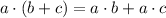
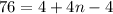
Simplify:

`76 = 4n`

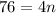
Divide both sides by 4 we have;

19 = n

or

n= 19

Substitute the given value and n = 19 in [2]

`S_(19) = (19)/(2)(4+76) = (19)/(2) \cdot 80 = 19 \cdot 40 = 760`

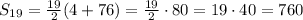
Therefore, the sum of the given finite arithmetic series is, 760