Question

A container is shaped like a cylinder with half spheres on each end. The cylinder has a length of 30 centimeters and a radius is 5 centimeters. To the nearest cubic centimeter, how many cubic centimeters can one container hold? Do not round calculations until the final answer.

Answer 1

`2880\text{ cm}^3`.

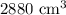Explanation:

We have been that a container is shaped like a cylinder with half spheres on each end. The cylinder has a length of 30 centimeters and a radius is 5 centimeters.

To find the volume of container we will use volume of container and volume of sphere formula.

Since half spheres are on the each side of cylinder, so adding them we will get one sphere.

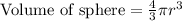`\text{Volume of sphere}=(4)/(3)\pi r^3`, where r represents radius of sphere.

`\text{Volume of sphere}=(4)/(3)*\pi*\text{(5 cm)}^3`

`\text{Volume of sphere}=(4)/(3)*\pi*125\text{ cm}^3`

`\text{Volume of sphere}=(500)/(3)\pi\text{ cm}^3`

`\text{Volume of sphere}=166.6666666\pi\text{ cm}^3`

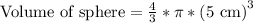
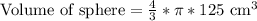
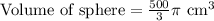
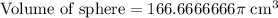
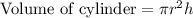`\text{Volume of cylinder}=\pi r^2h`, where r represents radius and h represents height of cylinder.

`\text{Volume of cylinder}=\pi*\text{ (5 cm)}^2*30\text{ cm}`

`\text{Volume of cylinder}=\pi*25\text{ cm}^2*30\text{ cm}`

`\text{Volume of cylinder}=750\pi\text{ cm}^3`

`\text{Volume of container}=750\pi\text{ cm}^3+166.6666666\pi\text{ cm}^3`

`\text{Volume of container}=916.6666666\pi\text{ cm}^3`

`\text{Volume of container}=2879.79326558120\text{ cm}^3\approx 2880\text{ cm}^3`

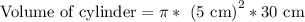
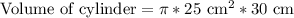
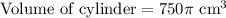
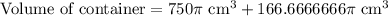
Therefore, the volume of our given container is
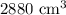`2880\text{ cm}^3`.

Answer 2

`2,880\ cm^(3)`

Explanation:

we know that

The volume of a container is equal to the volume of a cylinder plus the volume of one sphere

Step 1

Find the volume of a cylinder

The volume of a cylinder is equal to

`V=\pi r^(2) h`

we have

`r=5\ cm, h=30\ cm`

substitute

`V=\pi (5)^(2)(30)`

`V=750\pi\ cm^(3)`

Step 2

Find the volume of a sphere

The volume of a sphere is equal to

`V=(4)/(3)\pi r^(3)`

we have

`r=5\ cm`

substitute

`V=(4)/(3)\pi (5)^(3)`

`V=(500)/(3)\pi}\ cm^(3)`

Step 3

Find the volume of the container

`750\pi\ + (500)/(3)\pi}=2,879.79\ cm^(3)`

Round to the nearest cubic centimeter

`2,880\ cm^(3)`