Answer:
The correct option is 4.
Explanation:
If a line passing through two point, then the slope of the line is
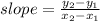
From the given table it is clear that the line passing through the points (4,26), (5,23) and (6,m).
Line passing through (4,26) and (5,23). So, the slope of the line is
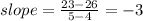
The slope of line is -3.
Line passing through (4,26) and (6,m), and the slope of the line is -3.
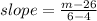
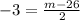
Multiply both sides by 2.
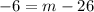
Add 26 on both the sides.
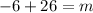
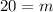
The value of m is 20 and because the rate of change is –3.
Therefore the correct option is 4.