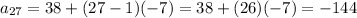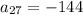Question

Identify the 27th term of an arithmetic sequence where a1 = 38 and a17 = −74

−20.5
−151
−22.75
−144

Answer 1

Hello : the general terme is : an = ap +(n-p)r..... n, p in N and r in R
let n=17 and p =1
a17 = a1+(17-1)r
-74 = 38 +16r
16r =-112
r = -7
an = a1 +(n-1)r
a27 =38+26(-7) =−144

Answer 2

`a_(27)= -144`

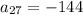
Explanation:

`a1=-38 \ and \ a_(17)= -74`

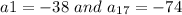
use arithmetic sequence to find the rule for nth term

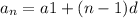`a_n= a1+ (n-1)d` where 'a1' is the first term and d is the difference

first term is 38

`a_17= 38+ (17-1)d`

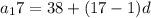
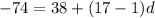`-74= 38+ (17-1)d` , solve for d

`-74= 38+16d`

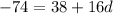
Subtract 38 from both sides

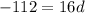`-112=16d`, divide both sides by 16

`d= -7`

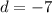
Now we find 26 term using a1= 38 and d=-7

`a_(27)= 38+ (27-1)(-7)=38+(26)(-7)=-144`

`a_(27)= -144`