Question

At a certain location, wind is blowing steadily at 10 m/s. Determine the mechanical energy of air per unit mass and the power generation potential of a wind turbine with 80-m-diameter (D) blades at that location. Take the air density to be 1.25 kg/m3. The mechanical energy of air per unit mass is kJ/kg. The power generation potential of the wind turbine is kW.

Answer 1

`0.05\ \text{kJ/kg}`

`3141.6\ \text{kW}`

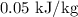
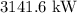
Step-by-step explanation:

v = Velocity of wind = 10 m/s

A = Swept area of blade =
`(\pi)/(4)d^2`

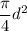
d = Diameter of turbine = 80 m

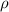`\rho` = Density of air =
`1.25\ \text{kg/m}^3`

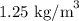
Wind energy per unit mass of air is given by

`E=(v^2)/(2)\\\Rightarrow E=(10^2)/(2)\\\Rightarrow E=50\ \text{J/kg}`

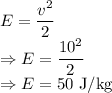
The mechanical energy of air per unit mass is
`0.05\ \text{kJ/kg}`

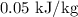
Power is given by

`P=\rho AvE\\\Rightarrow P=1.25* (\pi)/(4)* 80^2* 10* 50\\\Rightarrow P=3141592.65=3141.6\ \text{kW}`

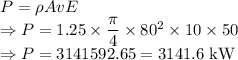
The power generation potential of the wind turbine is
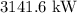`3141.6\ \text{kW}`.