Question

The first three terms of a geometric sequence are as follows.64, 32, 16Find the next two terms of this sequence.

Answer 1

The sequence is;

`64,32,16,\ldots`

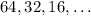
This is a geometric sequence of first term 64 and common difference 1/2,

Therefore, the nth term formula is;

`\begin{gathered} T_n=ar^(n-1) \\ a=64\text{ and r=}(1)/(2) \\ T_n=64((1)/(2))^(n-1) \end{gathered}`

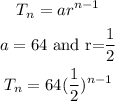
To obtain the fourth and fifth terms, we substitute n=4 and 5 into the equation;

`\begin{gathered} T_4=64((1)/(2))^3=8 \\ T_5=64((1)/(2))^4=4 \end{gathered}`

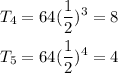
Therefore, the next terms of the sequence are 8 and 4.