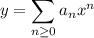
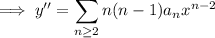
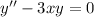
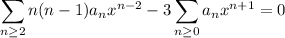
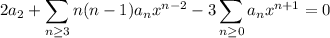
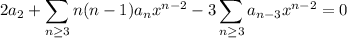
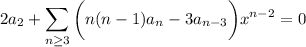
This generates the recurrence relation
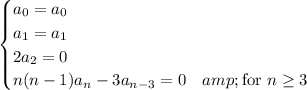
Because you have
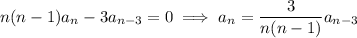
it follows that
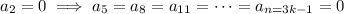
for all
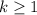
.
For
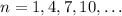
, you have
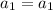
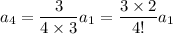
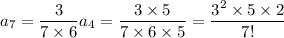
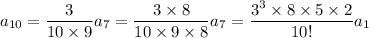
so that, in general, for
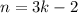
,
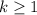
, you have
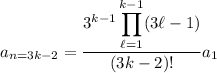
Now, for
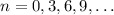
, you have
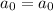
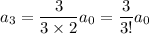
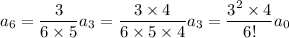
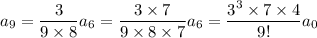
and so on, with a general pattern for
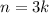
,
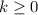
, of
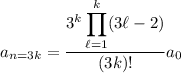
Putting everything together, we arrive at the solution
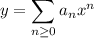
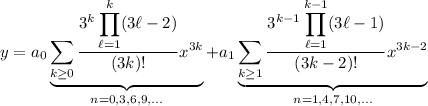
To show this solution is sufficient, I've attached is a plot of the solution taking
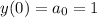
and
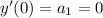
, with
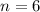
. (I was hoping to be able to attach an animation that shows the series solution (orange) converging rapidly to the exact solution (blue), but no such luck.)