Question

Rational and irrational numbers definition

Answer 1

all numbers that are not rational are considered a rational and irrational number can be written as a decimal, but not as a fraction.and irrational number has endless nonrepeating digits to the right of the decimal point

Answer 2

Rational numbers can be defined as numbers that can be written in fractional notation. Let's consider an arbitrary number
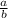
`(a)/(b)`, where a and b do not have common factors. This is an example of a rational number, as it can be described using a fraction. Real numbers and fractional numbers are among this branch of numbers.

Irrational numbers, on the other hand, are simply those numbers which cannot be written as an exact fraction, only approximated fractions. Famous cases of irrational numbers are those of π (pi), e (Euler's number/ Napier's constant), and many square root numbers.