Question

A heavy book is launched horizontally out a window from the first floor, a height, h, above the ground, with initial velocity, v0, and it hits the ground a horizontal distance X1 away from the window. Another book is similarly launched (same initial velocity) from the second floor window, a height 2h above the ground. Where does the second book land relative to the first book

Answer 1

x₂ / x₁ = √2

Step-by-step explanation:

To solve this exercise we can use the projectile launch ratios, let's find the time it takes for the second book to reach the ground

y = y₀ +
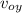`v_(oy)` t - ½ g t²

as the book is thrown horizontally v_{oy} = 0, when it reaches the ground its height is zero y= 0

0 = y₀ - ½ g t²

t =
`\sqrt{ (2y_o)/( g) }`

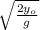
t = \sqrt{ \frac{2 \ 2h}{ g} }

with this time we calculate the horizontal distance traveled

x = v₀ t

x₂ = v₀
`\sqrt{ (4h)/(g) }`

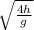
now let's calculate the time it takes him to get to the floor when he leaves from the first floor

t =\sqrt{ \frac{2y_o}{ g} }

the horizontal distance traveled is

x₁ = v₀
`\sqrt{ (2h)/(g) }`

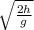
therefore the difference in distance between the two runs is

Δx = x₂-x₁

Δx = v₀ \sqrt{ \frac{4h}{g} } - v₀ \sqrt{ \frac{2h}{g} }

Δx = v₀ \sqrt{ \frac{2h}{g} } √2

Δx =√2 x₁

the relationship between the two distances is

x₂ / x₁ = √2