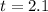Answer:
The value of the test statistic is
Explanation:
Our test statistic is:
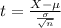
In which X is the sample mean,
 is the expected value,
is the expected value,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
The level of ozone normally found is 7.5 parts/million (ppm).
This means that
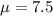
The mean of 24 samples is 7.8 ppm with a standard deviation of 0.7.
This means that

Test Statistic:
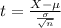
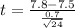
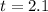
The value of the test statistic is