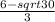Question

How do you get x-intercepts from this equation y=3x^2-12x+2?

Answer 1

Understand what it means when a question asks for x-intercepts. In a Cartesian plane, the x-intercept represents the x-coordinate for when it touches x-axis. It will always have a y-value of 0.

As such, substitute X(x, 0) into the equation to render: 0 = 3
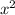
`x^(2)` - 12x + 2
Now, this becomes a quadratic, finding numbers that multiply to 6, and adds to -12. No numbers seem to fit, so you'll need to use the quadratic formula:


`\frac{-b +- sqrt{b^2 - 4ac}}{2a}` becomes

`\frac{12 +- sqrt{144 - 24}}{6}`

When we're dealing with quadratic formulae, we need to understand where it comes from.
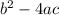
`b^(2) - 4ac` is our discriminant and we use this a lot in future mathematics. For now, we'll understand the power of the quadratic formula. Let's consider a standard equation of a line: ax + by + c = 0, where a, b and c all represent arbitrary constants.

The discriminant ensures that we will have a root. If the discriminant is less than zero, it's not that there are no roots, they aren't real (if you study complex numbers, you will understand), but because we're dealing with real numbers, the discriminant ensures that there are roots that are real.


`\frac{12 +- sqrt{120}}{6}` =
`\frac{12 +- 2sqrt{30}}{6}` =
`\frac{6 +- sqrt{30}}{3}`

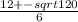
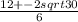
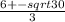
And our x-intercepts become:
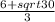
`\frac{6 + sqrt{30}}{3}` and
`\frac{6 - sqrt{30}}{3}`