Question

A loan used for buying a home is called a mortgage. The

Fernandez family is buying a
$375,000 home. They are taking
out a 30-year mortgage at a rate of 8%.
a. Compute the monthly payment.
b. Find the total of all of the monthly payments for the 30
years.
c. What is the finance charge?
d. Which is greater, the interest or the original cost of the
home.

Answer 1

a. The monthly payment is approximately $2,751.62

b. The total of all monthly payment for the 30 years is approximately $990,582.175

c. The finance charge is approximately $615,582.175

d. The interest is greater than the original cost of the home

Explanation:

a. The given parameters for the mortgage are;

The principal amount of the home Fernandez family is buying, P = $375,000

The number of years mortgage they take buy the home = 30 years

The percentage rate of the mortgage, r = 8%

The monthly payment, 'A', for the mortgage is given as follows;

`A = ( P * \left ((r)/(12) \right ) *\left (1 + (r)/(12) \right )^n)/(\left (1 + (r)/(12) \right )^n - 1 )`

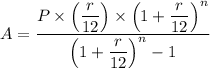
Where;

n = The number of monthly payments = 30 years × 12 months/year = 360 months

Therefore, by substituting the known values, we have;

`A = ( 375,000 * \left ((0.08)/(12) \right ) *\left (1 + (0.08)/(12) \right )^(360))/(\left (1 + (0.08)/(12) \right )^(360) - 1 ) = 2,751.61715172`

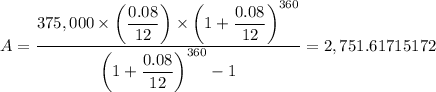
The monthly payment, A = $2,751.61715172 ≈ $2,751.62

b. The total of all monthly payment for the 30 years = 360 × $2,751.61715172 ≈ $990,582.175

c. The finance charge = The total amount repaid - The amount that was financed = The interest payed on the amount financed

∴ The finance charge = $990,582.175 - $375,000 ≈ $615,582.175

d. The interest (approximately $615,582.175) is greater than the original cost of the home ($375,000)