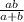There are two ways you can go about this: I'll explain both ways.
Solution 1: Using logarithmic properties
The first way is to use logarithmic properties.
We can take the natural logarithm to all three terms to utilise our exponents.
Hence, ln2ᵃ = ln5ᵇ = ln10ⁿ becomes:
aln2 = bln5 = nln10.
What's so neat about ln10 is that it's ln(5·2).
Using our logarithmic rule (log(ab) = log(a) + log(b),
we can rewrite it as aln2 = bln5 = n(ln2 + ln5)
Since it's equal (given to us), we can let it all equal to another variable "c".
So, c = aln2 = bln5 = n(ln2 + ln5) and the reason why we do this, is so that we may find ln2 and ln5 respectively.
c = aln2; ln2 =
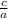
c = bln5; ln5 =
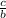
Hence, c = n(ln2 + ln5) = n(
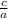 +
+
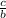 )
)
Factorise c outside on the right hand side.
c = cn(
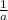 +
+
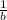 )
)
1 = n(
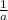 +
+
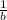 )
)
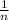 =
=
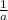 +
+
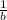
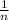 =
=
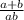
and thus, n =
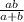
Solution 2: Using exponent rules
In this solution, we'll be taking advantage of exponents.
So, let c = 2ᵃ = 5ᵇ = 10ⁿ
Since c = 2ᵃ, 2 =
![\sqrt[a]{c}](https://img.qammunity.org/2018/formulas/mathematics/high-school/zlv66hotjqnghjc583rih2rd79ovd3zg81.png) =
=
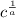
Then, 5 =

and 10 =
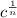
But, 10 = 5·2, so 10 =
 ·
·
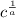
∴
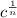 =
=
 ·
·
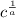
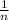 =
=
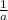 +
+
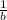
and n =