ANSWER
The volume of the oxygen gas is 17.5 L
Step-by-step explanation
Given that;
The mass of oxygen gas is 12 grams
The temperature of the gas is 25 degrees Celcius
The pressure of the gas is 53 kPa
To find the volume of the oxygen gas, follow the steps below
Step 1; Assume the gas behaves like an ideal gas
Therefore, apply the ideal gas equation to find the volume of the gas
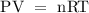
Where
P is the pressure of the gas
V is the volume of the gas
n is number of moles of the gas
R is the universal gas constant
T is the temperature of the gas
Step 2: Find the number of moles of the oxygen gas using the below formula
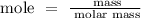
Recall, that the molar mass of the oxygen gas is 32 g/mol
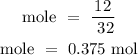
Step 3; Convert the temperature to degree Kelvin
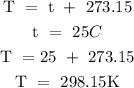
Step 4; Substitute the given data into the formula in step 1
Recall, that R is 8.314 L kPa K^-1 mol^-1

Hence, the volume of the oxygen gas is 17.5 L