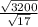Question

A fence is to be built to enclose a rectangular area of 320 square feet. The fence along three sides is to be made of material that costs 5 dollars per foot, and the material for the fourth side costs 12 dollars per foot. Find the dimensions of the enclosure that is most economical to construct.

Answer 1

For these questions, we need to form a general equation that satisfies the conditions given.
We know:
A = 320ft²
3 fences - 5 dollars per foot and 1 fence - 12 dollars per foot.

A = 320 = xy

Eliminate one variable and solve for that:
x =
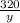
`(320)/(y)` (1)

We need to now find an equation for the amount of money we are going to spend.

We can visualise it in our heads: We have two short sides to be built and two long sides to be built. One side will cost us 12 dollars, while the other three costs just 5 dollars to build.

We can now find our perimeter, which is given by 2x + 2y, but we know that x can be replaced as
`(320)/(y)`.

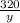
Hence, our perimeter becomes: 2(
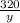
`(320)/(y)`) + 2y.
Now, let's write an equation for C(y), where C is our total cost.

C(y) = 5*(2*
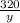
`(320)/(y)` + y) + 12y) = 10*
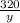
`(320)/(y)` + 5y + 12y =
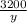
`(3200)/(y)` + 17y

Now, we want to find when it's a minimum so that it will cost us the least amount of money.
Take the first derivative, and let it equal to 0.

C'(y) = -3200*y⁻² + 17 = 0

`(-3200)/(y²)` = -17

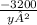
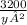
`(3200)/(y²)` = 17

3200 = 17y²
y² =
`(3200)/(17)`
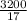
y =
`(√(3200))/(√(17))`

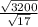
Now, to prove that it's a min. at y =
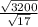
`(√(3200))/(√(17))`, take the second derivative:

C''(y) = 3200y⁻³ and at y =
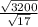
`(√(3200))/(√(17))`, C''(y) > 0 and therefore, min. amount used.

So, at y =
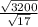
`(√(3200))/(√(17))`, it will be the least amount of money spent.

Substitute y, back into (1) to find for x.

x =
`(320)/((√(3200))/(√(17)))`

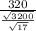
therefore, x =
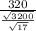
`(320)/((√(3200))/(√(17)))` and y =
`(√(3200))/(√(17))`