Question

In the electric currect​ flow, it is found that the resistance​ (measured in the units called​ ohms) offered by a fixed length of wire of a given material varies inversely as the square of the diameter of the wire. If a wire 0.01 in. in diameter has a resistance of 0.331 0.331 ​ohm, what is the resistance of a wire of the same length and material with diameter 0.0182 0.0182 in. to the nearest​ ten-thousandth?

Answer 1

The resistance of a wire varies inversely as the square of the wire's diameter. To find the resistance of a second wire, we use the formula R1 * d1^2 = R2 * d2^2 and solve for R2.

Step-by-step explanation:

The resistance of a wire varies inversely as the square of the diameter of the wire. So if a wire with a diameter of 0.01 inches has a resistance of 0.331 ohms, we can establish a relationship between resistance (R) and diameter (d) according to this inverse square law: R1 * d12 = R2 * d22, where R1 and R2 are the resistances of the wires and d1 and d2 are their respective diameters.

Using the given values, we have:
0.331 * (0.01)2 = R2 * (0.0182)2

Solving for R2 gives us:
R2 = (0.331 * (0.01)2) / (0.0182)2 ohms

By calculating R2 with the specified diameters, we can determine the resistance of the second wire.

Answer 2

`\bf \begin{array}{llllll} \textit{something}&&\textit{varies inversely to}&\textit{something else}\\ \quad \\ \textit{something}&=&\cfrac{{{\textit{some value}}}}{}&\cfrac{}{\textit{something else}}\\ \quad \\ y&=&\cfrac{{{\textit{k}}}}{}&\cfrac{}{x} &&y=\cfrac{{{ k}}}{x} \end{array}`

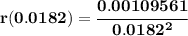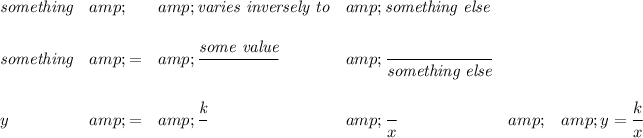
so... when something varies inversely in relation to something else, usually means y = k/x or thereabouts, with "k" the constant of variation, being a constant divided by the denominator

so, in this case the resistance say "r", varies inversely to the square of the diameter "d", that simply means
`\bf r(d)=\cfrac{k}{d^2}`
so, what the dickens is "k" then?

now, we know that, the resistance is 0.01 when the diameter is 0.331

that simply means
`\bf 0.01=\cfrac{k}{0.331^2}\implies 0.01\cdot 0.331^2=k\implies 0.00109561=k \\\\\\ \textit{that means, the equation is really }r(d)=\cfrac{0.00109561}{d^2}`

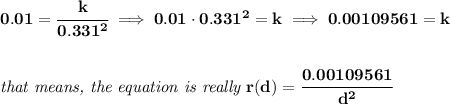
now... what is the resistance "r" when d=0.0182? well,
`\bf r(0.0182)=\cfrac{0.00109561}{0.0182^2}`