Question

How do you find the volume and surface area of this??

Answer 1

You multiply 2 (m) and 0.8 (m) by each other and then use that answer and multiply it by the sides (faces) that the object contains :P

Answer 2

if you check the picture below, the figure is just an octagonal prism, namely, a regular octagon solid

so... notice the picture, the figure itself is just 2 regular octagons, stacked up to 8 rectangles at the corners

so just get the area of the octagons, and the area of the rectangles, and add them up together, that's the area of the figure

area of a rectangle, you surely know how to get

now, to get the area of a regular polygon
`\bf \textit{area of a regular polygon}\\\\ A=\cfrac{1}{4}\cdot n\cdot s^2\cdot cot\left( (180)/(n) \right)\qquad \begin{cases} n=\textit{sides in the polygon}\\ s=\textit{length of one of sides} \end{cases}`

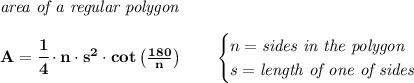
notice, for your figure, is an OCTA=8, gon, so 8 sides, n = 8, and the side's length is 0.8

---------------------------------------------------------------------------------

now. the volume is simple, the volume of it, will just be the area you found for the octagon times the height
namely (area of octagon) * (2)