Answer:
Maximum length and breadth of the box is 6.32 cm and the height of the box is 3.16 cm
Explanation:
Surface area of box
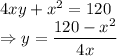
Volume of box is
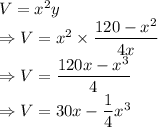
Differentiating with respect to


Equating with zero
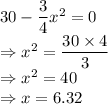
Double derivative of the volume
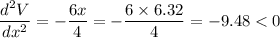
So, the volume is maximum at
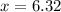
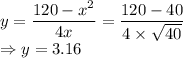
So, the maximum length and breadth of the box is 6.32 cm and the height of the box is 3.16 cm.