Answer:
Line y = −x + 4 intersects the line y = 3x + 3.
Explanation:
The given system of equations is
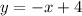
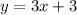
In graphical method of solving linear system of equations, we plot the graph of the given equations. The intersection point of the graphs would give the solution.
The slope of the first line is -1
And the slope of the second line is 3
The slopes are not equal. Hence, the line are not parallel.
When we plot the graphs of these equations then the intersection point will give us the solution.
The intersection point is (0.25,3.75).
Hence, the solution is x=0.25, y=3.75
Therefore, first option is correct.