Question

Please help? Graph
`-3x^2+12y^2=84`. Find domain and range.

I have the graph, but I don't know how to find the domain and range?

Answer 1

`-3x^2+12y^2=84`

`12y^2=3x^2+84`

`y^2=\frac{x^2}4+7`

`y=\pm\sqrt{\frac{x^2}4+7}`

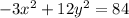
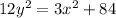
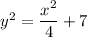
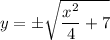
For either square root to exist, you require that
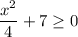
`\frac{x^2}4+7\ge0`. This is true for all
`x`, since
`\frac{x^2}4` is always non-negative. This means the domain of
`y` as a function of
`x` is all real numbers, or
`x\in\mathbb R` or
`(-\infty,infty)`.

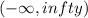
Now, because
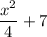
`\frac{x^2}4+7` is non-negative, and the smallest value it can take on is 7, it follows that the minimum value for the positive square root must be
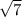
`\sqrt7`, while the maximum value of the negative root must be
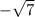
`-\sqrt7`. This means the range is
`y\in\mathbb R\setminus(-\sqrt7,\sqrt7)`, or
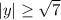
`|y|\ge\sqrt7`, or
`(-\infty,-\sqrt7]\cup[\sqrt7,\infty)`.