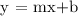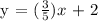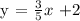Let us first solve for the slope (m) of the perpendicular line.
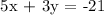
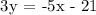

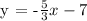
The slope of the perpendicular line is -5/3.
Thus, for the slope of the line, we get,
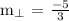

Let us solve for the value of b with the given value of slope (m) = 3/5 and (x,y) = (-5,1).
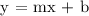
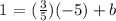
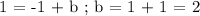
Let's now make the equation of the line using Slope-Intercept Form,
Given, m = 3/5 and b = 2